| [1] |
张毅, 梁兆新. 自旋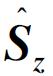 旋转至 旋转至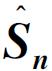 的相似变换可视化[J]. 大学物理, 2023, 42(8): 55-. 的相似变换可视化[J]. 大学物理, 2023, 42(8): 55-. |
| [2] |
林正喆, 陈熙. 对经典力学中的轨道角动量和自转角动量的探讨[J]. 大学物理, 2022, 41(8): 15-. |
| [3] |
江少钦, 余雪佳, 徐莉梅. 无序复杂系统中的序⎯2021 年诺贝尔物理学奖解读[J]. 大学物理, 2022, 41(2): 7-. |
| [4] |
董正高. 复杂电磁波的动量密度[J]. 大学物理, 2022, 41(12): 26-. |
| [5] |
傅洪波, 陈小伟, 谢国喜. 磁共振成像K空间信号的数理模型——以自旋回波序列为例[J]. 大学物理, 2022, 41(12): 39-. |
| [6] |
郑兴荣, 郑燕飞. N 维势箱函数量子特性的可视化研究[J]. 大学物理, 2022, 41(1): 19-. |
| [7] |
杨 一, 李秀玲, 罗成林. 托马斯效应的简单诠释[J]. 大学物理, 2021, 40(5): 71-. |
| [8] |
袁喆. 固体物理教学的若干思考Ⅱ: 磁学前沿案例[J]. 大学物理, 2021, 40(4): 1-5. |
| [9] |
金芳洲, 彭玉平, 李庆容, 朱小飞. 玻恩规则的实验检验
[J]. 大学物理, 2021, 40(12): 29-. |
| [10] |
闫二斌. 论角动量的态空间[J]. 大学物理, 2021, 40(10): 18-. |
| [11] |
林琼桂. 磁单极场中的空间转动对称性与轨道角动量[J]. 大学物理, 2020, 39(10): 1-4. |
| [12] |
马 遥, 庞 蜜. 半导体中电子回旋共振有效质量的量子理论推导[J]. 大学物理, 2020, 39(07): 29-31. |
| [13] |
程剑剑, 郑华. 电子自旋是角动量的讨论[J]. 大学物理, 2019, 38(10): 28-. |
| [14] |
路峻岭,顾晨,秦联华,任乃敬. 关于夏天中伏天数的探究[J]. 大学物理, 2018, 37(6): 41-44. |
| [15] |
罗国忠. 随时间变化的磁场对电子自旋的量子控制[J]. 大学物理, 2018, 37(12): 1-. |